10.8- Equations of Circles

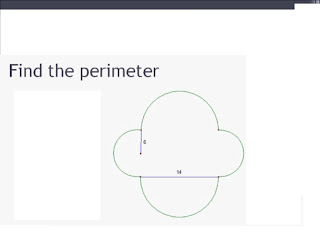
    Before watching the video didn’t know anything about the equations of circles. The only thing that I knew was what a circle was.

    After watching the video I learned about the standard form of a circle. It is x minus h to the second plus y minus k to the second equals r to the second. H and K is the center of the circle and r is the radius of the circle. So, you can use this in order to find the radius of the circle. For example, if the center is five and negative one and there is a point on the circle that is one, two, you can plug that into the equation r equals the square root of x-h to the second plus y minus k to the second and get you radius. So, after you add and subtract your information after plugging it in, you get the radius to equal the square root of negative four to the second plus three to the second. After you square the numbers you get r to equal the square root of sixteen plus nine, or the square root of twenty-five. The square root of twenty-five is five, so your radius equals five. Lastly you plug that into the standard form and get your equation to be x minus five to the second plus y minus one to the second equation five to the second, or twenty-five. You can also graph the equation onto a graph, so basically you are doing the opposite; you are given the equation and you have to graph it. This is everything that I learned about after watching the video.

Word Count: 276

Questions:

I commented on Adam B's blog and ........

10.7- Segment Lengths in Circles

     

      Before watching the video the only things that I knew about was that I knew what a secant and a tangent were. There is nothing else that I knew about before watching the video.

     After watching the video I learned about three different theorems. The first one is the chord intersection theorem. The chord intersection theorem is if two chords intersect in the interior of a circle, then the product of the segments of one chord equals the product of the other segments. If secant CD and secant AB intersect in the same spot in circle E, then you have EA multiplied by EB equals EC multiplied by ED. The second/third theorems are the external secant and tangent theorems. The second one deals with secants and secants and the third one deals with secants and tangents. So, the secant and secant theorem is if two secants share the same endpoint outside a circle, then the products of the external segment and the whole segment equals the other product of the external and whole segment. So, if secant AB and secant CD have the same endpoint outside of the circle, which is point E, then EA multiplied by EB equals EC multiplied by ED. The last theorem is the secant and tangent theorem. That is if a secant and a tangent share an endpoint outside a circle, then the tangent segment squared equals the product of the external and internal segments of the secant. So, if tangent EA and secant ED share the same endpoint outside the circle, which is point E, then EA squared equals EC multiplied by ED. This is everything that I learned about after watching the video.

Word Count: 280

Questions:

I commented on Brittany Boettcher's blog and Tori Lemke's blog.

10.6- Angles Relationships

     

      Before the video I knew what tangents, chords, and secants were. This is all I knew about before watching the video.
      After watching video I learned about the tangent/chord theorem. The tangent/chord theorem is if a tangent and a chord intersect on a circle, then the measures of the angles formed are half of the intercepted arcs. So, measure of angle one equals half of measure of arc AB. You can use this to find the measures of angles and arcs. I also learned about the chord intersection theorem. The chord intersection theorem is if two chords intersect in the interior of a circle, then the measure of each angle is half the sum of the intercepted arcs and its vertical angle. So, the measure of angle one equals half of measure of arc CD plus measure of arc AB, or measure of angle two equals half of measure of arc BC plus measure of arc AD. You can use this to find the measures of arcs and the measure of angles. The last theorem I learned about was the secant/tangent intersection theorems. The secant/tangent intersection theorem is if a tangent and secant, two tangents, or two secants intersect in the exterior of a circle, then the measure of each angle is half the difference of the measure of the intercepted arc. So, there are three equations; one for the tangent and secant, one for the secant and secant, and one for the tangent and tangent. The tangent and secant equation is measure of angle one equals half of measure of arc BC minus measure of arc AC. For secant and secant the equation is measure of angle two equals half of measure of arc XY minus of measure of arc WZ. Lastly, for tangent and tangent the equation is measure of angle three equals half of measure of arc XY minus measure of arc WZ. You can use these three equations to find the measure of arc and measure of angles, but you have to make sure you are using the right equation. This is everything that I learned in the video.

Word Count: 353

Questions:

I commented on Leah S.'s blog and Christina B's blog.

10.5-Tangets to Circles

                                                                   


      Things that I knew before the video were that I knew what a center, radius, diameter, and a chord were. This is all that I knew about before watching the video.
      Things that I learned about after watching the video were that I learned about what a secant and a tangent were. I also learned about the three different ways circles can intersect. They can intersect each other at two points, one point, or not at all. If they don’t intersect at all, they are called concentric circles. I also learned about common tangents. A common tangent is a line tangent to two or more circles. There are also tangent theorems. One is if m is tangent to circle Q at P, then m is perpendicular to line QP and vise versa (if m is perpendicular to line QP, then m is tangent to circle Q at P). You can use this to find out if there is a tangent to a circle and to find out the radius of a circle. Another tangent theorem is if line SR and line ST are tangent to circle P, then line SR is congruent to line ST. You can use this to find the value of X when you are given the length of ‘ST’ and ‘SR’. This is everything that I learned about after watching the video.

Word Count: 226

Questions:

I commented on Riley Eickert's and Leah S.'s blogs.

10.4-Inscribed Angles

    I didn’t know anything before I watched this video.

    Some of the things I learned after watching the video were the inscribed angle theorem. The inscribed angle theorem is when an angle goes through a circle the measure of the angle equals have of the arc it intersects. For example, if angle ABC equals thirteen, then arc AC equals twenty six because angle ABC equals half of twenty six. So, you multiply thirteen by two. Another thing that I learned was about the multiple intercepted arcs theorem. That is if two inscribed angles of a circle intercept the same one, then the angles are congruent. So, if angle CAD intersect arc CD and angle CBD also intersects arc CD, then angle A is congruent to angle B. The inscribed right triangle theorem is another theorem I learned about. This theorem is when a right triangle is inscribed in a circle if and only if the hypotenuse of the triangle is a diameter of the circle. So, if right triangle ACB is in circle D, then the hypotenuse AB has to be a diameter of circle D. If it is, then the right triangle is a inscribed right triangle. The last theorem I learned about was the inscribed quadrilateral theorem. The inscribed quadrilateral theorem is when a quadrilateral can be inscribed in a circle if and only if the opposite angles are supplementary. For example if quadrilateral ABCD is in circle E, then angle measure of angle A plus measure of angle C equals 180 and measure of angle B plus measure of angle D equals 180 in order for the quadrilateral to be an inscribed quadrilateral. You can use all of these theorems to find angle measure in the specific triangle that you are given. This is all I learned in the video about Inscribed Angles.   

Word Count: 306

Questions:

I commented on Tori Lemke's and Brittany Boettcher's blogs.

10.2-Measuring Angles and Arcs

    The only thing that I knew before the video was what an arc was and that was the only thing that I knew about before watching the video.
    I learned about the sum of central angles. The sum of central angles is the sum of the measures of the central angles of a circle with no interior points in common is 360. An example is the measure of angle one plus the measure of angle two plus the measure of angle three equals 360. Also I learned about minor arcs, major arcs, and semicircles. A minor arc is the shortest arc connecting two endpoints on a circle. The measure of it is less than 180 and equal to the measure of its related central angle. A major arc is the longest arc connecting two endpoints on a circle. The measure of a major arc is greater than 180 and equal to 180 minus the measure of the minor arc with the same endpoints. A semicircle is an arc with endpoints that lie on a diameter. The measure of a semicircle always equals 180. You can use the sum of central angles, minor arcs, major arcs, and semicircles to find measures of central angles and the value of different angles. Also, I learned about the arc addition postulate. The arc addition postulate is when two arcs added together give you the measure of the two combining arcs. For example the measure of arc ABC equals the measure of arc AB plus the measure of arc BC. You can use this to find the measures of arcs. I also learned about an equation that can help you find the measures of arc lengths, finding the central angle/arc measures, and to find the circumference. The equation is arc AB equals (the measure of arc AB divided by 360) times 2πr. Lastly, I learned about how to find the perimeter of different objects.

Word Count: 319

Questions:

1.) Can someone explain the questions at the end of the video (the perimeters ones)? I don't get how to do it.

2.) On slide 21 can someone explain how to get the circumference? I don't get it.

10.1-Circles and Circumference

Before the video I knew about the formulas for finding the circumference, radius, and diameter of a circle. Also, I knew about the different parts of a circle (diameter, chord, and radius). Lastly, I knew about how to find the radius and diameter and this is all I knew before the video.

After the video I learned about congruent circles and concentric circles (coplanar circles). For two circles to be congruent, the two circles have to have congruent radii. For two circles to be concentric circles (coplanar circles), they have to have the same center. I also learned about finding measures in intersecting circles. Like one of the questions in the video had you find the length of XY. You where given the diameter of circle X and the diameter of circle Y, which is twenty-two and sixteen. Lastly, you were given the length of WZ, which is five. First, you have to find the radius of the two circles. To find the radius you can use the diameter formula, which is diameter = 2 * radius. Let’s find the radius of circle X. Since you have the diameter of circle X. You plug it in the formula and get 22=2r. Then, you divide 22/2 and get your radius to equal 11. You do the same thing to circle Y and get the radius to equal 8. So, you add 6+5+3 and get 14. So, 14 is the length of XY. The last thing I learned was about finding the exact circumference. All you have to do is find the circumference, but instead of multiplying it by π, you just leave it. For example, if the radius is 6, the formula would look like this: C=2π(6). Then, you multiply 2 times 6 and get 12. So, your exact circumference would be 12π.

Word Count: 302

Questions:

1.) Can someone explain how to get the answer to the question on slide 11? I don’t get it.

2.) Can someone explain how to get the answer to the question on slide 15? I don’t get it.